También llamado sistema decimal, es un sistema de numeración posicional en el que las cantidades se representan utilizando como base aritmética las potencias del número diez. El conjunto de símbolos utilizado (sistema de numeración arábiga) se compone de diez cifras diferentes: cero (0); uno (1); dos(2); tres (3); cuatro (4); cinco (5); seis (6); siete (7); ocho (8) y nueve (9).
62 (10) = 6*10^1 + 2*10^0
60 2
62
Sistema de numeración binaria:
En matemáticas e informática, es un sistema de numeración en el que los números se representan utilizando solamente las cifras cero y uno (0 y 1). Es el que se utiliza en las computadoras, debido a que trabajan internamente con dos niveles de voltaje, por lo cual su sistema de numeración natural es el sistema binario (encendido 1, apagado 0).
Sistema de numeración octal
El sistema numérico en base 8 se llama octal y utiliza los dígitos 0 a 7.
Para convertir un número en base decimal a base octal se divide por 8 sucesivamente hasta llegar a cociente 0, y los restos de las divisiones en orden inverso indican el número en octal. Para pasar de base 8 a base decimal, solo hay que multiplicar cada cifra por 8 elevado a la posición de la cifra, y sumar el resultado.
Es más fácil pasar de binario a octal, porque solo hay que agrupar de 3 en 3 los dígitos binarios, así, el número 74 (en decimal) es 1001010 (en binario), lo agruparíamos como 1 / 001 / 010, después obtenemos el número en decimal de cada uno de los números en binario obtenidos: 1=1, 001=1 y 010=2. De modo que el número decimal 74 en octal es 112.
Sistema de numeración hexadecimal:
Es un sistema de numeración que emplea 16 símbolos. Su uso actual está muy vinculado a la informática y ciencias de la computación, pues los computadores suelen utilizar el byte u octeto como unidad básica de memoria; y, debido a que un byte representa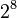 
valores posibles, y esto puede representarse como
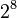valores posibles, y esto puede representarse como
Según el teorema general de la numeración posicional, equivale al número en base 16 
, dos dígitos hexadecimales corresponden exactamente —permiten representar la misma línea de enteros— a un byte.
, dos dígitos hexadecimales corresponden exactamente —permiten representar la misma línea de enteros— a un byte.| Hexadecimal | Decimal |
|---|---|
| A | 10 |
| B | 11 |
| C | 12 |
| D | 13 |
| E | 14 |
| F | 15 |
No hay comentarios:
Publicar un comentario